최단 경로(Shortest Path) 1 - 다익스트라 알고리즘(Dijkstra's Algorithm)

Algorithm
AlgorithmBellman-FordDijkstraFloyd-WarshallGraphShortest Path

다익스트라 알고리즘(Dijkstra’s Algorithm)

최단 거리를 구하는 방법 중 가장 유명한 알고리즘이라고 할 수 있는 다익스트라 알고리즘은 Edsger Dijkstra가 고안했으며 시작 정점을 제외한 다른 모든 정점에 이르는 최단 경로를 구하며 음의 가중치를 허용하지 않는다.

BFS exmaple

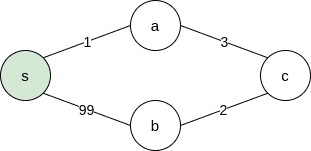
다익스트라의 알고리즘은 BFS와 유사한 형태로 시작점에서 가까운 순서로 정점을 방문한다. 일례로 위 그림에서 BFS로 탐색을 한다면 시작점에서 가까운 정점부터 탐색을 하기 때문에 s-a-b-c가 되지만 실제로는 s-a-c-b가 최단경로가 된다. 나중에 방문한 정점의 간선의 가중치가 더 작을 수 있기 때문에 이 문제를 해결하기 위해 다익스트라 알고리즘은 큐(queue) 대신 우선 순위 큐(priority queue)를 이용한다.

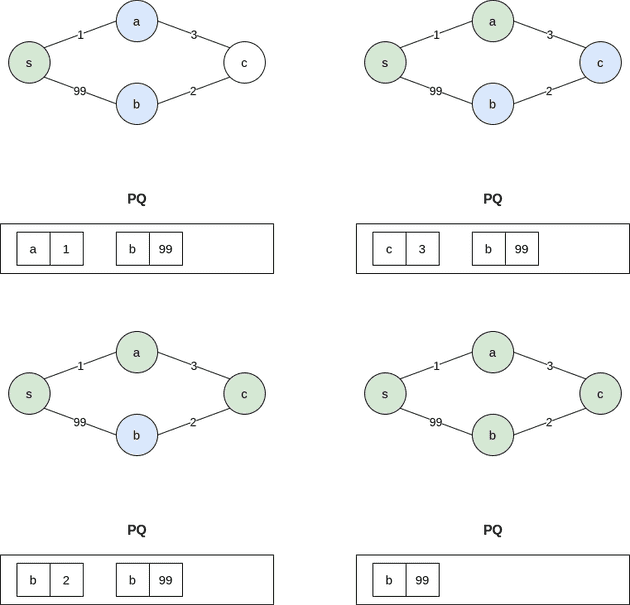
BFS에서는 큐에 인접한 정점을 추가했다면 다익스트라에서는 찾아낸 해당 정점까지의 최단거리를 쌍으로 넣는다. 우선 순위 큐는 정점까지의 최단 거리를 기준으로 정점의 순서를 정렬하고 방문하지 않은 정점 중 시작점으로부터의 거리가 가장 가까운 정점을 찾게 해준다.

PQ

위의 그림으로 예시를 들면 우선 순위 큐에 변화를 보면 정점 c와 정점 b가 연결될 때 기존의 s에서 b로가는 거리보다 짧다. 이 경우 우선 순위 큐에 남아 있는 (b, 99)을 처리해야 하는데 다음과 같은 방법을 이용한다.

  • 우선 순위 큐에서 (b, 99)를 (b, 6)으로 바꾼다.
  • (b, 99)가 큐에서 나올 때 무시한다.

전자는 구현도 어렵고 대부분의 STL에서 지원지 않으므로 보통은 후자의 방법을 많이 쓴다. 이 경우 이미 존재하는 최단 경로의 길이 보다 크다면 무시하면 된다.

구현

다익스트라의 원래 알고리즘은 O(V2)O(V^2)의 시간복잡도를 가지지만 우선 순위 큐를 이용하면 O(ElogE)O(ElogE)에 해결할 수 있다. 여기서는 우선 순위 큐를 이용한 방법을 토대로 구현해보았다.

const Dijkstra = (graph, begin) => {
    const pq = new MinHeap(null);
    const dist = Array(V + 1).fill(Infinity);
    dist[begin] = 0;
    pq.insert([begin, 0]);

    while (pq.heap.length > 0) {
        const [node, weight] = pq.pop();
        if (dist[node] < weight) continue;

        for (let [nextNode, nextWeight] of graph[node]) {
            const weightSum = weight + nextWeight;
            if (dist[nextNode] > weightSum) {
                dist[nextNode] = weightSum;
                pq.insert([nextNode, weightSum])
            }
        }
    }
    return dist;
};

먼저 이진 힙을 이용해서 우선 순위 큐를 구성하고 각 정점들까지의 최단 거리를 담는 dist 배열을 시작 정점을 제외하고 Infinity로 초기화 해주었다. 이후 우선 순위 큐도 시작 정점에 대해 초기화를 해준다.

이후 우선 순위 큐에 원소들이 남아 있을 동안 반복을 진행하며 만약 현재 추출한 [정점, 가중치] 쌍이 가진 가중치가 기존의 최단 거리보다 크다면 무시하고 그렇지 않다면 계속해서 진행한다.

현재 정점에 인접한 정점들을 탐색하여 대상 정점이 갖는 기존의 최단 거리보다 현재 정점으로 오는 가중치와 다음 정점으로 향하는 가중치의 합이 더 작다면 그 값으로 대체하고 우선 순위 큐에 [정점, 새로운 가중치] 쌍의 형태로 넣어준다.

참고로 모양새가 프림 알고리즘(Prim’s algorithm)과 비슷하게 생겼다. 최소 신장 트리나 프림에 관련된 것은 이 포스트에서 확인할 수 있다.

Default graph

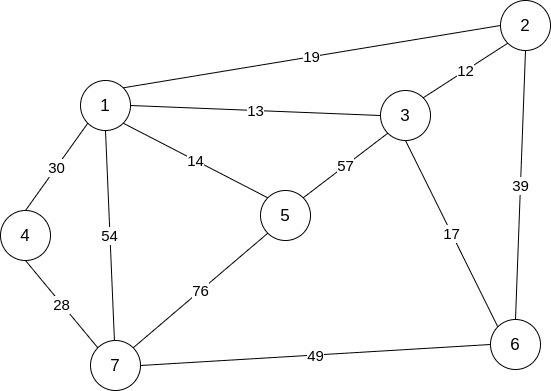
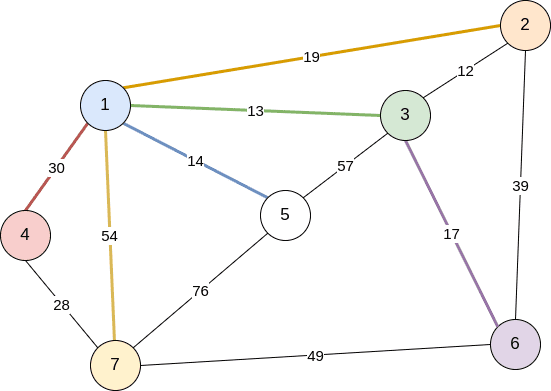
위와 같은 그래프를 5번 정점을 시작 정점으로 정하고 다익스트라를 통해 최단 거리를 구해 보면 다음과 같은 결과가 나온다.

Default graph

시간 복잡도 분석

  • 각 정점은 한 번씩 방문되고 각 정점에 인접한 간선들에 대해 한 번씩 검사하므로 O(E)O(E)가 걸릴 수 있다.
  • 우선 순위 큐에 들어갈수 있는 최대 원소의 크기는 EE이며 우선 순위 큐를 수선하는 작업은 O(logE)O(logE) 이므로 모든 원소에 대해서 해당 작업을 반복한다면 O(ElogE)O(ElogE)가 될 수 있다.

O(E+ElogE)O(E + ElogE)

중복 원소를 우선 순위 큐에 넣지 않도록 하여 O(VlogV)O(VlogV)에 수행 가능하다고 한다. 그러나 실제로는 구현의 복잡도나 오버헤드때문에 잘 쓰지 않는다고 한다.

결과

Solved

백준 최단경로 문제의 결과이다.

참조(References)