유니온-파인드(Union-Find)

Algorithm
AlgorithmData StructureDisjoint SetTreeUnion-Find

유니온-파인드

유니온-파인드(union-find)는 트리형 자료 구조의 일종으로 일반적인 트리의 형태와는 조금 다르다. 상호 배타적인 집합을 다루기 때문에 서로소 집합(disjoint set)이라고도 부르며 서로소 부분 집합들로 나뉘어진 원소들에 대한 정보를 저장하고 조작하는 자료구조이다. 이를 통해 그래프에서 어떤 노드가 같은 집합에 있는지 확인할 수 있다. 상호 배타적이기 때문에 두 집합의 교집합은 공집합이기 때문에 교집합연산은 필요없다. 해당 자료구조에서 필요한 연산은 다음 3가지이다.

  • MakeSet(x)MakeSet(x): 원소 xx를 집합으로 만든다.
  • Find(x)Find(x): 원소 xx를 가진 집합을 찾는다.
  • Union(x,y)Union(x, y): 두 원소 xx와 yy를 하나의 집합으로 만든다.

연결리스트로 구현

Linked-List

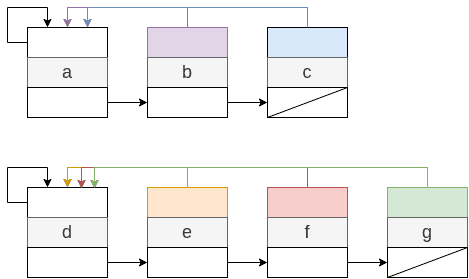
{a, b, c}를 원소로 가지는 집합 A와 {d, e, f, g}를 원소로 가지는 집합 B가 있다. 각 집합이 속하는 대표 원소를 향하는 포인터와 같은 집합에 속하는 다음 원소의 주소를 가리키는 포인터가 하나씩 있다. 만약 다음 노드가 없다면 NIL을 가리키면 된다.

Linked-List2

두 집합 A와 B를 합치는 union 연산을 할 때 큰 집합에 작은 집합을 이어 붙이면 된다. 당연하게도 작은 집합의 원소 개수가 더 적기 때문에 대표 원소로 포인터를 옮기는 작업이 적기 때문이다. 작은 집합의 대표 원소의 포인터를 큰 집합의 대표 원소의 주소를 가리키게 하고 큰 집합의 마지막 노드의 다음 노드를 작은 집합의 대표 원소를 가리키면 된다. 이와 같은 방법은 무게를 고려한(weighted) union이라한다.

이 방법에서 시간 복잡도는 makeSet과 find연산은 O(1)O(1)에 가능하고 weighted union 연산 중 m번의 makeSet, union,, find 연산을 수행 할 때 n번이 makeSet이라면 O(m+nlogn)O(m + nlogn)에 가능하다.

트리로 구현

연결 리스트로 구현하는 것보다 더욱 효율적인 방법이 있는데 각 집합을 하나의 트리로 구현하는 것이다. 일반적인 트리의 경우 부모 노드가 자식 노드를 가리키지만 여기서는 자식 노드가 부모 노드를 가리킨다. 하나의 원소를 가지는 집합에 대해 노드를 만들고 부모 노드가 있는 경우 부모 노드를 가리키고 없는 경우 스스로를 가리킨다.

Naive Disjoint Set

Union Find Tree

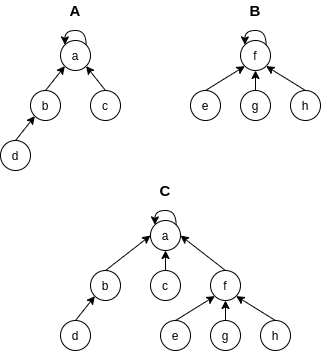
두 집합 {a, b, c, d}와 {e, f, g, h}를 union할 경우 단순히 한 집합의 루트 노드의 부모를 다른 집합의 루트 노드로 변경해주면 된다. 이 때 두 원소가 같은 집합에 포함되는지 확인 하기 위해서는 트리의 루트 노드를 확인하면 된다. 따라서 트리에서 find 연산은 같은 루트 노드를 갖는지 확인하는 작업을 거치면 된다. union에서는 찾은 두 루트 노드 중 하나의 루트 노드를 다른 하나의 루트 노드를 가리키게 하면 된다.

class DisjointSet {
    constructor() {
        this.set = [];
    }

    makeSet(n) {
        for (let i = 0; i < n; i += 1) {
            this.set[i] = i;
        }
    }

    union(u, v) {
        u = this.find(u), v = this.find(v);
        if (u === v) return;
        this.set[u] = v;
    }

    find(u) {
        if (u === this.set[u]) return u;
        return this.find(this.set[u]);
    }
}
  • 초기화를 하는 makeSet에서는 각 노드가 스스로를 가리키도록 하는 과정이다.
  • find는 찾고자 하는 원소의 값이 루트 노드인 경우 바로 반환하고 그렇지 않으면 부모 노드를 재귀적으로 호출한다.
  • union은 합치고자 하는 두 노드의 루트 노드를 찾아서 한 루트 노드의 부모 노드의 주소를 다른 루트노드로 변경한다.

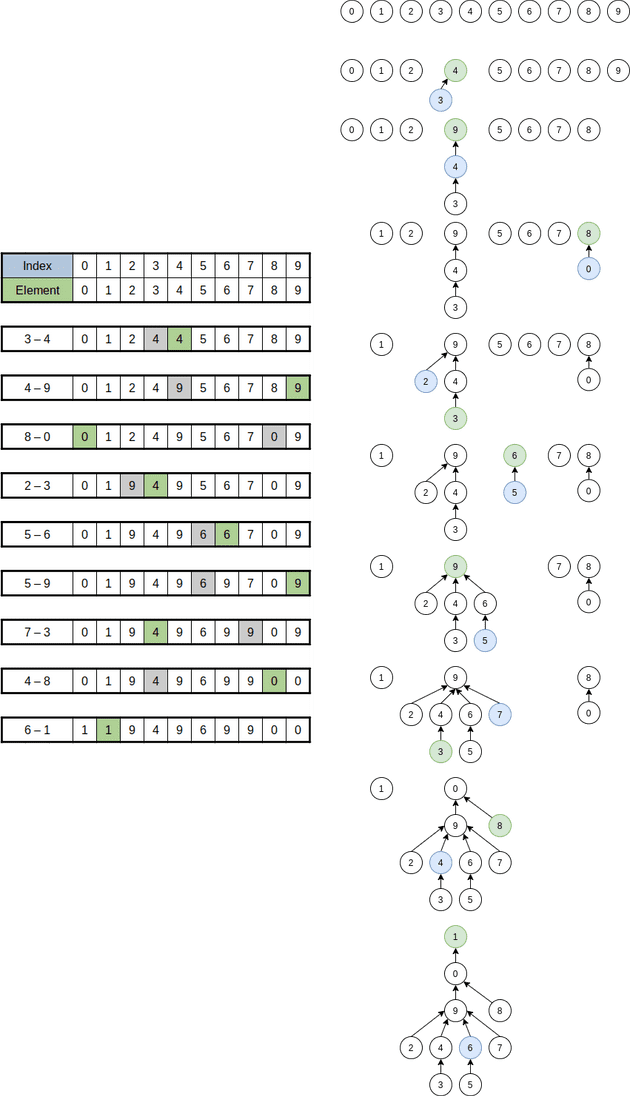
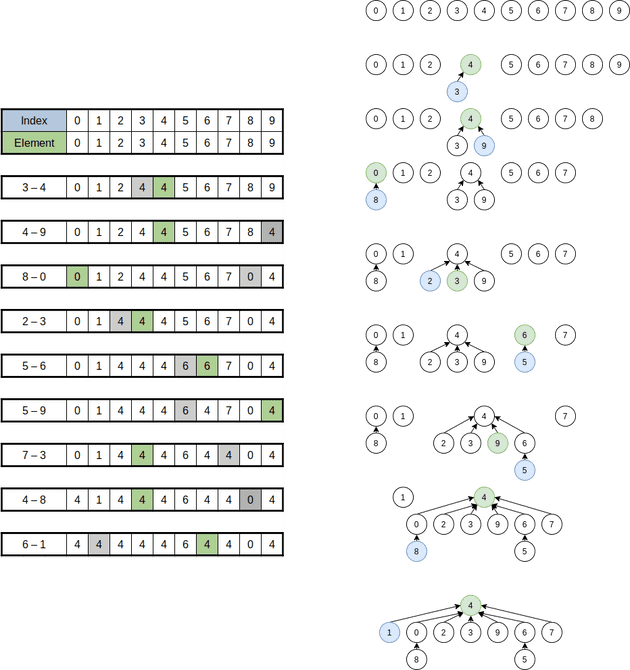
아래 그림은 해당 코드의 일련의 진행 과정을 나타낸 것으로 배열의 인덱스는 노드를 뜻하고 배열의 원소는 해당 노드의 부모 노드를 가리킨다. 3 - 4의 뜻은 union(3, 4)와 같다.

Quick Union

Weighted Union

앞선 구현에서는 find와 union을 실행하는 데 걸리는 시간은 트리의 높이에 비례한다. 다만 이 방법은 이진 트리와 같이 연산 순서에 따라 한쪽으로 편향된 트리의 모습이 될 수도있다. 이 해결책으로는 여러가지 방법이 있는데 그 중 하나가 항상 높이가 더 낮은 트리를 높이가 더 큰 트리 밑에 집어넣는 것이다. 이러한 최적화를 앞서 말한 weighted union라 부른다. 각 노드가 자신을 루트로 하는 서브 트리의 높이를 rank라 부르고 단 하나의 노드로 된 트리의 경우 rank는 0이다.

Union Find Tree with Rank

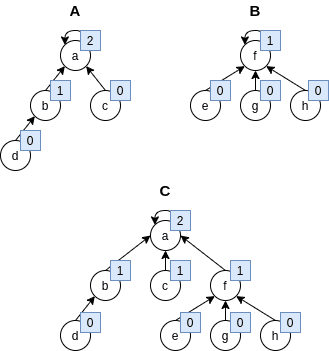
각 노드에 랭크를 표시했다. 집합 A와 B를 합치기 위해 전체 랭크가 1인 B집합을 전체 랭크가 2인 A 집합에 붙였고 전체 랭크의 크기는 늘어나지 않았다. 합치는 두 집합의 랭크가 같은 경우에만 전체 랭크의 크기가 커진다.

class DisjointSet {
    constructor() {
        this.set = [];
        this.rank = [];
    }

    makeSet(n) {
        for (let i = 0; i < n; i += 1) {
            this.set[i] = i;
            this.rank[i] = 0;
        }
    }

    union(u, v) {
        u = this.find(u), v = this.find(v);
        if (this.rank[u] > this.rank[v]) {
            this.set[v] = u;
        }
        else {
            this.set[u] = v;
            if (this.rank[u] === this.rank[v]) {
                this.rank[v] += 1;
            }
        }
    }

    find(u) {
        if (u === this.set[u]) return u;
        return this.find(this.set[u]);
    }
}

weighted union 을 이용하기 위해 기존 코드에 몇 가지를 추가했다.

  • makeSet에 랭크 값을 담는 배열을 0으로 초기화 해준다.
  • union 실행시 u 의 랭크가 더 크다면 v를 u의 서브 트리로 추가한다.
  • v가 더 크거나 같다면 u를 v의 서브 트리로 추가하고 둘의 랭크가 같다면 랭크 값을 증가 시킨다.

Weighted Union

앞선 일반적인 union-find보다 트리의 높이가 낮아진 것을 확인할 수 있다. 높이가 h인 트리가 생기기 위해서는 h-1인 트리 2개가 합쳐져야 한다. h가 1이면 0인 노드 2개가 필요하고 h가 2이면 h가 1인 노드가 최소 2개는 필요하다. 따라서 h-1의 높이를 가지기 위해 n개의 노드가 필요하다면 h의 높이를 갖기 위해서는 최소 2n개의 노드가 필요하다. 즉, 높이가 h일 때 노드의 개수는 최소 2h2^h개 이므로 노드의 개수가 n개라면 h=lognh = logn이 된다. 따라서 탐색과 병합 연산은 O(logn)O(logn)이 된다.

Path Compression

다른 최적화 방법도 있는데, weighted union이 합치는 단계에서 시간을 절약한다면 경로 압축(path compression)은 탐색하는 과정에서 시간을 줄이는 방법이다.

Path Compression

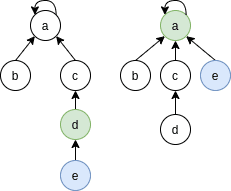
위 그림을 보면 좌측의 e 노드의 경우 d - c - a 순서로 부모를 탐색해나간다. 탐색을 한 번 수행 했으므로 다음 번 e 노드의 루트 노드를 바로 a 노드로 바꾸어 준다면 다음 번 e를 탐색할 때 불필요한 과정을 거칠 필요가 없는 것이다.

find(u) {
    if (u === this.set[u]) return u;
    return this.set[u] = find(this.set[u]);
}

find(u)를 통해 u가 속하는 루트 노드를 찾았을 때 그 값을 반환하고 그렇지 않을 경우 루트 노드를 찾을 때 까지 재귀적으로 호출하여 루트 노드를 갱신한다.

Weighted Union with Path Compression

두 가지 최적화를 모두 적용한 경우, n개의 원소에 대해 union-find를 m번 수행했을 때 평균 시간 복잡도가 O(mlog∗n)O(mlog^*n)이라고 한다.

log∗n=min(k∣loglog...logn<=1)log^*n = min(k | loglog...logn <= 1)

log∗nlog^*n은 nn에 loglog를 k번 적용할 때 1이하가 된다는 뜻으로, Ackermann fucntion와 관련이 있다. 간략히 말하면 다룰 수 있는 모든 수에 대해 5보다 작으며 평균적으로 상수 시간이 걸린다.

최종 코드

class DisjointSet {
    constructor() {
        this.set = [];
        this.rank = [];
        this.size = 0;
    }

    makeSet(n) {
        for (let i = 0; i < n; i += 1) {
            this.set[i] = i;
            this.rank[i] = 0;
        }
        this.size = this.rank.length;
    }

    union(u, v) {
        u = this.find(u), v = this.find(v);
        if (this.rank[u] > this.rank[v]) {
            this.set[v] = u;
        }
        else {
            this.set[u] = v;
            if (this.rank[u] === this.rank[v]) {
                this.rank[v] += 1;
            }
        }
    }

    find(u) {
        if (u === this.set[u]) return u;
        return this.set[u] = this.find(this.set[u]);
    }
}

참조(References)